Limits to Growth and the Malthusian Trap
Limits to Growth
Limits to Growth
The Malthusian Trap
Two historical myths
Discussion
Topics discussed
How scarce resources limit population and income
But also influence inequalities
How the Malthusian trap was escaped
An old intuition
Malthus (food production), Ricardo (decreasing return to agriculture)
Jevons (depletion of coal, the fuel for industrial revolution, 1865)
Mr & Mrs Meadows (natural resources depletion)
- Club of Rome,1968 report from MIT researcher (futurologists)
- The Limits to Growth carries a wide review of natural resources, assess reserves and explore 5 exponential trends demographic, means of subsistence production, industrialization, pollution, consumption of finite resources (oil, but many others)
- 2004 : Limits to Growth : The 30 Year Update
Each time, technology, price & behaviour responses have pushed back the limits. Far away.
But we need to go further this simple scheme
- Unified growth (Galor, Kremer)
- Pomeranz, Barbier and Californian Economic History School
The Malthusian Trap
Limits to Growth
The Malthusian Trap
Two historical myths
Discussion
Overview - the Unified Growth Model
Imagine that you need a minimum income (consumption) to live : absolute poverty (2$/day) i.e. what is needed to keep you alive and sustain your productive capacity
Let’s call it starvation income (SI)
- Population dynamics (evolution over time) will depend on current income relative to SI.
- Human ecology and population dynamics are similar to other living beings.
- First hypothesized by Malthus, inspired Darwin, Spencer and others.
- A major breakthrough: humans are not God’s creature
One of the first general equilibrium analysis
- Malthus concludes that to fight poverty, you need to stop charity and reduce the birthrate of poor people (i.e. the poor have to marry before sex)
- Malthus is the first neo-conservative: science and reason at the service of religious morality and commands.
- Reconciliation between old and enlightment morals
Technically, population is endogenous in a growth model
Some references on the Unified Growth Model
- Lucas, R.E Jr, 1999, “The industrial revolution: past and future”, Mimeo, Department of economics, University of Chicago
- Galor O. and Weil D.N., 2000. “Population , Technology , and Growth : From Malthusian Stagnation to the Demographic Transition and beyond”, The American Economic Review, 90(4), 806–828.
- Galor O., 2010. “The 2008 Lawrence R. Klein lecture - comparative economic development: Insights from unified growth theory”, International Economic Review, 51(1), 1–44.
Components of the Malthusian Trap
Population dynamics
- If current income (CI) > SI population increases (less mortality, more fertility)
- Reverse if SI > CI
- Special case : population control
Decreasing returns in production of land and fixed quantity of land
- Land is a non-accumulated factor
- Land productivity is decreasing
- More labor implies more output
- More input yields more output but less than proportionally (decreasing returns)
- AKA decreasing marginal productivity
- Because of decreasing returns, population is limited
- At some point, when adding a worker, output is going to increase by less than what is needed to feed the additional worker
Exogenous shocks can increase output
More land is discovered, new techniques (seeds, irrigation, rotation of culture, fertilizers, mechanization) can increase the output per unit of surface (and unit of work)
What is going to happen to:
- output? population? output per person?
- mean and median output per person?
- Inequalities?
Graphical representation
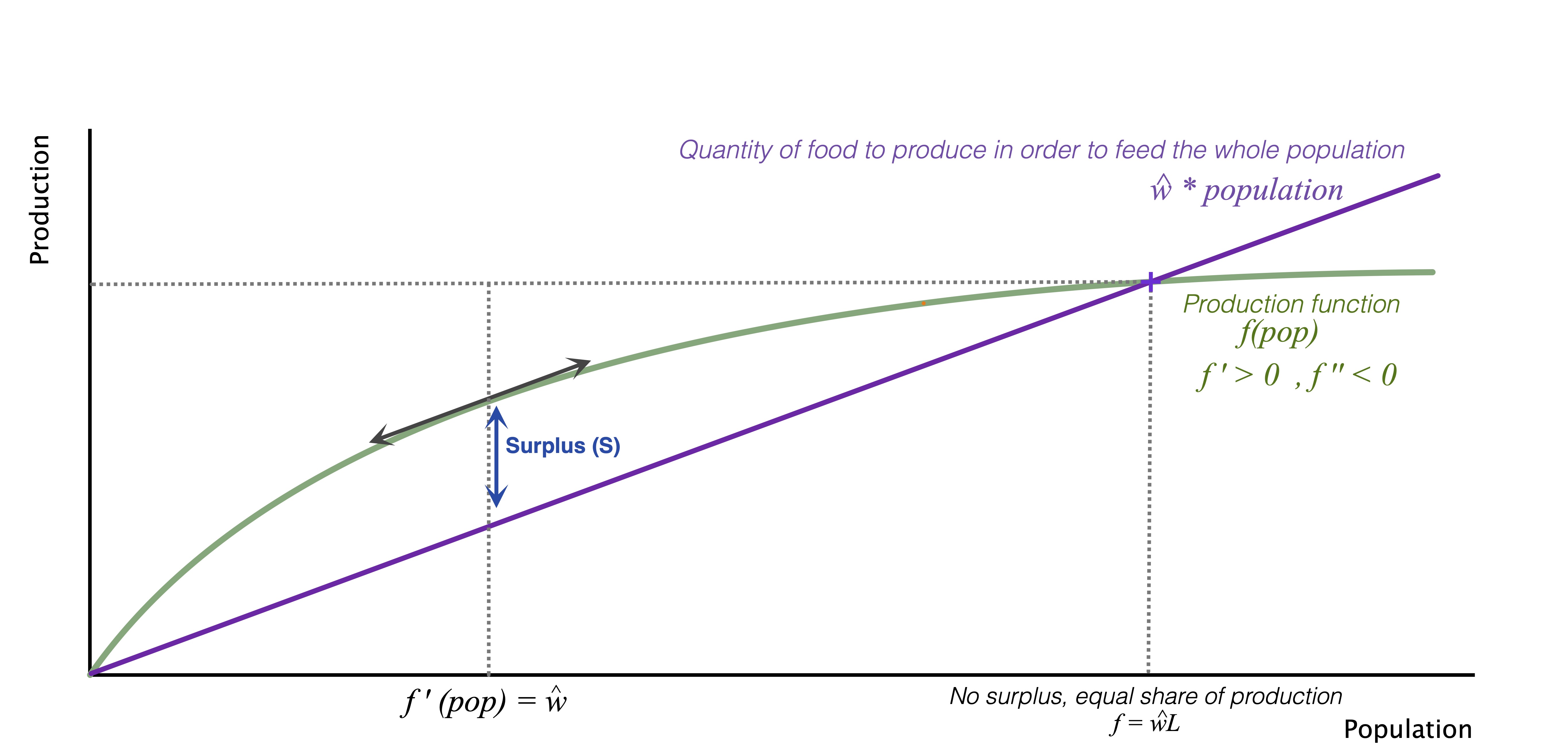
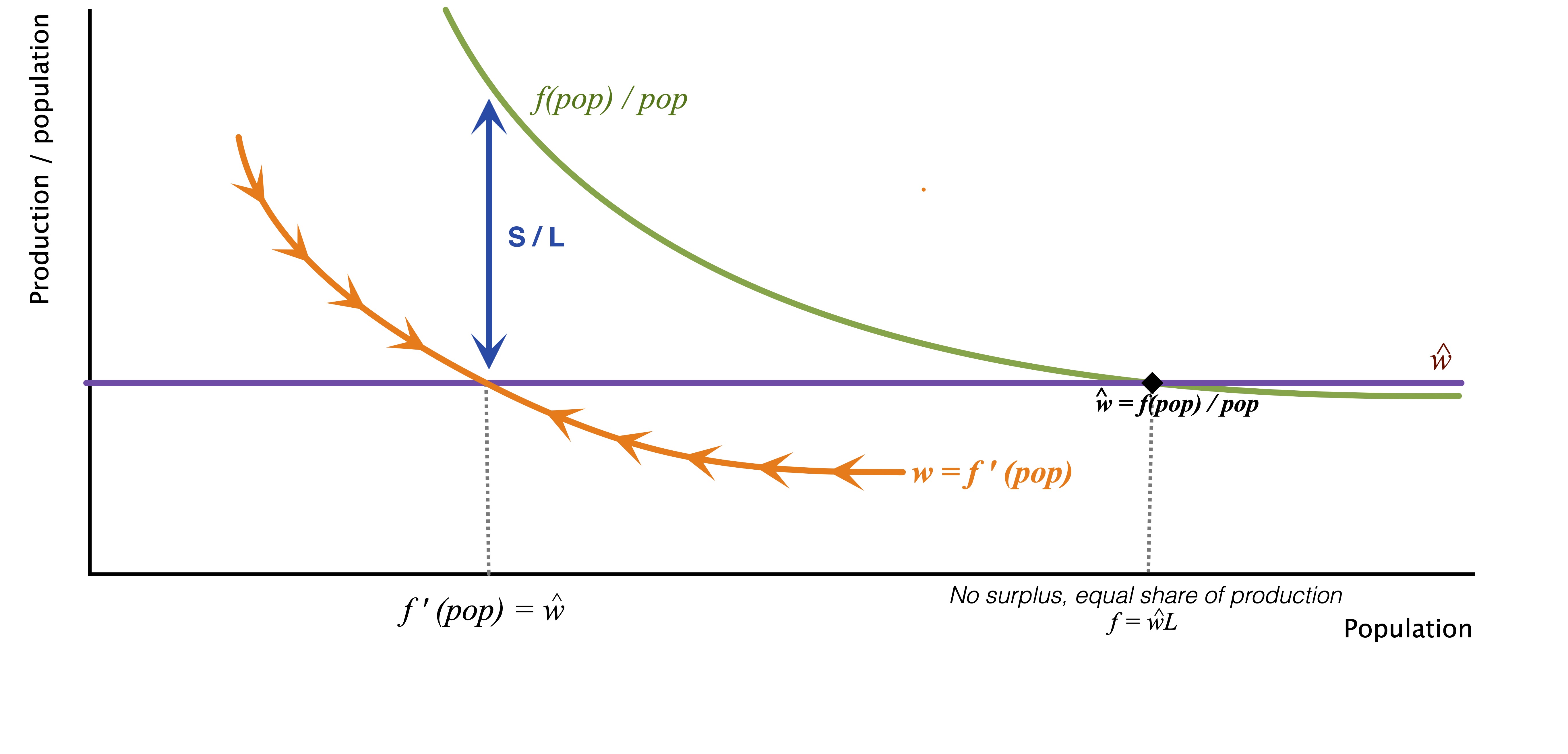
Suppose a usual Cobb-Douglas production function \[f(K,L) = A K^\alpha L^{1-\alpha} , 0 < \alpha < 1 \]
\(K\) stands for capital (i.e. land resources), with a fixed quantity.
\(L\) stands for labour, unit is an individual, and for simplicity \(L\) is equal to the population (no one is inactive)
\(w\) is the wage, with \(\widehat{w}\) the starvation income (minimum income needed to not die)
\(S\) is the surplus : \(S = f - wL\)
\[\frac{f}{pop} = \frac{f}{L} =\frac{AK^\alpha}{L^\alpha}\] is a decreasing function of \(L\)
In a competitive labour market:
\[w=f_L^\prime= (1 - \alpha) \frac{f}{L} < \frac{f}{L}\] Equilibrium population in a competitive market: \[L^*= \left(\frac{(1−𝛼)𝐴}{\widehat{w}}\right)^{\frac{1}{\alpha}}K\]
Full share equilibrium:
\[L^{**}=\left(\frac{A}{\widehat{w}}\right)^{\frac{1}{\alpha}}K=\frac{L^*}{(1-\alpha)^{\frac{1}{\alpha}}} > L^*\] When \(f_L^\prime = \widehat{w}\) , then \(S = \frac{\alpha}{1-\alpha}\widehat{w}L^* > 0\)
The higher the \(\alpha\), the higher the surplus.
How to observe a change in population
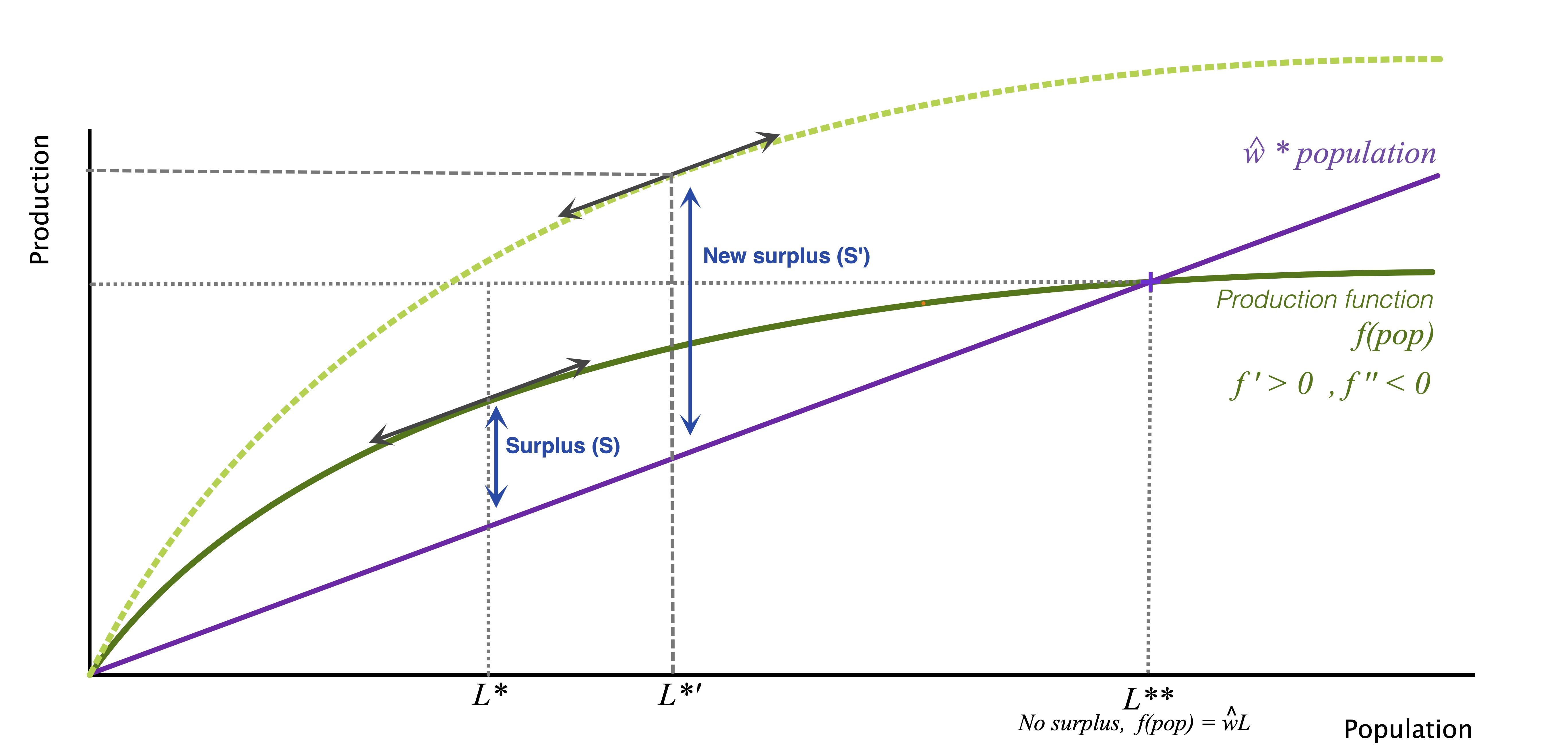
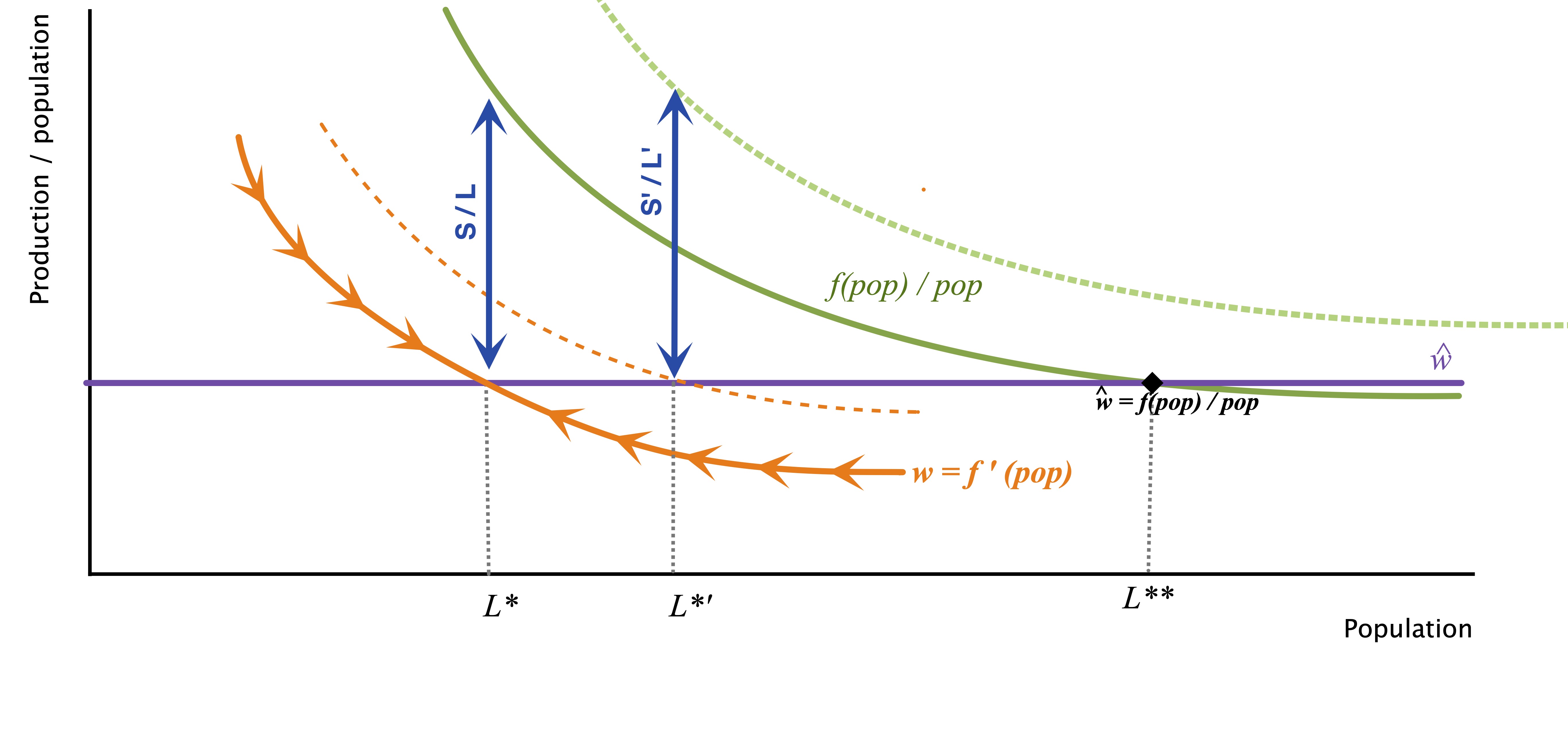
An increase in \(K\) (i.e. more land) or in \(A\) (technical progress) will shift the production function upwards .
- Population is going to increase :
\[L^*= \left(\frac{(1−𝛼)𝐴}{\widehat{w}}\right)^{\frac{1}{\alpha}}K\]
- And surplus is going to increase
\[ S = \frac{\alpha}{1-\alpha}\widehat{w}L^* = \alpha \left(\frac{1-\alpha}{\widehat{w}}\right)^{\frac{1-\alpha}{\alpha}} A^{\frac{1}{\alpha}}K\]
- However, wages remain unchanged (and equal to \(\widehat{w}\))
From property to starvation

Starvation is a fixed point
- Population dynamic is key
- Average product is the sum of marginal product (per head) and surplus (per head). Marginal production per head is equal to starvation income, is median income and is constant (i.e., independent of 𝐾 or of 𝐴)
- The gap between mean and median income is inequality
Property of land implies surplus
- Fixed quantity of land and increasing population means inequality
A “robust” model from 10 000 BC to circa 1750 AD
- Malthus didn’t anticipate exit from the trap
- His only conclusion was population control
No sex before marriage, especially for the poor
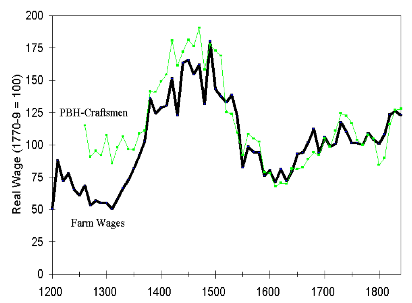
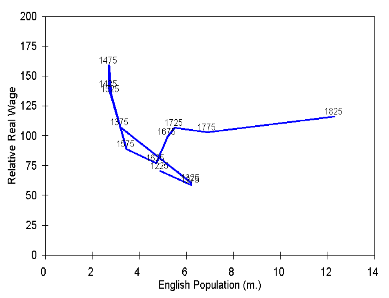
England in the Trap
Source: Clark, G., Rogers, J. E. T., Beveridge, W., Gilboy, E., & Phelps-brown, H. (1850). THE LONG MARCH OF HISTORY : FARM LABORERS ’ WAGES IN ENGLAND 1208-1850, 1–35.
Wages are built using various sources, based on archive data, manuscript wages statement, and so on. Cost of living is based on price information about grains.
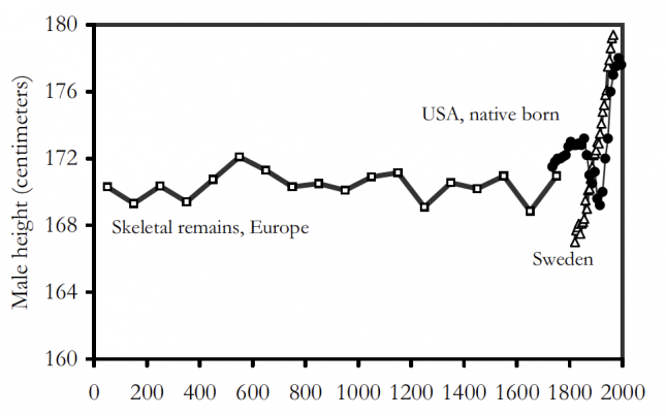
Are you a Malthusian ?
Inequality Possibility Frontier
Inequality and level of development revisited
The IPF
The IPF (inequality Possibility Frontier) is built as :
- Everyone has \(\widehat{w}\), except one who has everything else: \(f - \widehat{w}L\)
The Gini coefficient:
0 means equal allocation
1 means 0 for everyone and the remainder goes to one person
IPF: everyone gets \(\widehat{w}\) , and the rest for one person (maximum inequality possible)
When total production increases, the IPF increases
Inequality and level of development revisited quiz 1
Inequality and level of development revisited quiz 2
Escaping the Malthusian Trap
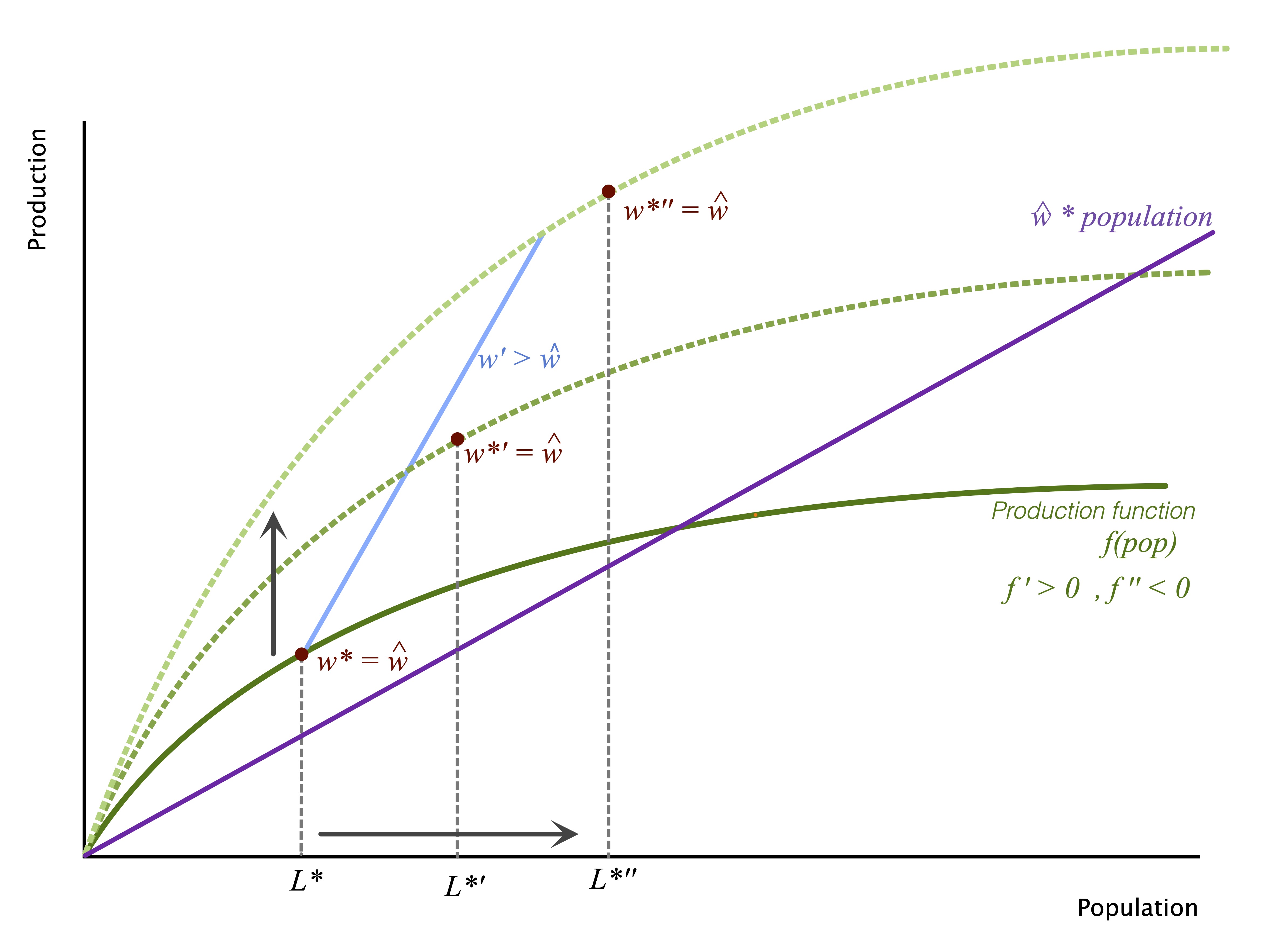
Imagine a production shift “faster” than the increase in population:
- faster means than population does not succeed to reach population equilibrium
Then, population is lagging for equilibrium population
- There is room (through market forces) for wage increase above \(\widehat w\), the starvation income
Then median food/population can rise, and starvation is no more a “point fixe”
Widespread (by the median individual) accumulation is made possible
- Increases individual productivity, participate in shifting the production function, self-sustained dynamics
positive feedback loop #1
The demographic transition
Accumulation of capital means wealth
Split of inheritance between descendants implies fewer children per couple
Demographic transition decrease in the rate of growth of population
Equally, accumulation of capital needs specific human capital, children are costlier to educate and have a higher return (i.e. they can take care of their parents).
positive feedback loop #2
And it continues
Positive feedback loops make the escape from the Malthusian trap faster and faster
Innovations, fueled by new markets and demand for new goods
Mechanization and chemistry of agriculture was an important leap
Increase in productivity of agriculture made possible the advent of industry
Population shifting from agricultural sector to industrial sector, new products appear
Increase in individual wealth shift institutions toward private property protection
more positive feedback loops
Important consequences
Land is no more a fixed asset and is a produced asset
Property of a produced asset is not the same as property of a non produced one
Produced asset can be socially (i.e. artificially) made scarce
Visualizing the escape from the trap
Two historical myths
Limits to Growth
The Malthusian Trap
Two historical myths
Discussion
Abel and Cain

Source: Tintoretto
The Death of Remus and the end of Pastoralism

Discussion
Limits to Growth
The Malthusian Trap
Two historical myths
Discussion
The modernity of Malthusian trap
What lessons would you draw from the Malthusian trap model ?
Land may not be scarce in the future, but what else could be ?
What could be done when facing scarcities ?


Limits to Growth and the Malthusian Trap EoE 2025: The Age of Constraints